不等式组平面区域画法
友情提醒:由于黑边网站宽度限制,上传文本可能存在页面排版较乱的情况,如果点击下载或全屏查看效果更佳。查看本科目或其他科目更多知识点。
简单线性规划问题是高考必考知识点,而其基础在于研究二元一次不等式(组)所对应的平面区域.下面介绍一些方法来快速准确地确定二元一次不等式(组)所表示的平面区域。
知识点总结

本节在段考中,主要是以选择题和填空题的形式考查二元一次不等式组合简单的线性规划问题的基础知识,以解答题的形式考查简单的线性规划问题的应用。在高考中各种题型都有出现,主要是考查简单的线性规划问题。
1、画不等式对应的平面区域时,有时容易边界问题。有等号,要把边界画成实线,没有等号,要把边界画成虚线。
2、注意不要列错了线性约束条件。
方法一:直线定界,特殊点定域
找出一个二元一次不等式(组)在平面直角坐标系内所表示的平面区域的基本方法是:
①画直线 ②取特殊点
②取特殊点 ③代值定域
③代值定域 ④求公共部分
④求公共部分
①画直线──作出各不等式对应方程表示的直线(原不等式带等号的作实线,否则作虚线);
②取特殊点──平面直角坐标系内的直线要么过原点,要么不过原点;当直线过原点时我们选取特殊点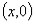 或
或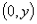 (坐标轴上的点),当直线不过原点时我们选取原点
(坐标轴上的点),当直线不过原点时我们选取原点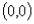 做特殊点;
做特殊点;
③代值定域──将选取的特殊点代入所给不等式:如果不等式成立,则不等式所表示的平面区域就是该特殊点所在的区域;如果不等式不成立,则不等式所表示的平面区域就是该特殊点所在区域的另一边.
④求公共部分──不等式组所确定的平面区域,是各个二元一次不等式所表示平面区域的公共部分.
例1 画出不等式组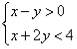 所表示的平面区域.
所表示的平面区域.
解析:①画直线:不等式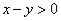 对应的直线方程是
对应的直线方程是 ;不等式
;不等式 对应的直线方程是
对应的直线方程是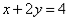 ;在平面直角坐标系中作出直线
;在平面直角坐标系中作出直线 与
与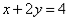 (如图).
(如图).
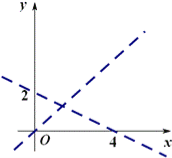
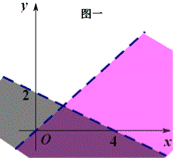
②取特殊点:直线 过原点,可取特殊点
过原点,可取特殊点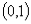 ;直线
;直线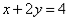 不过原点,可取特殊点
不过原点,可取特殊点 .
.
③将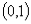 代入,即
代入,即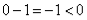 ,不等式
,不等式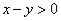 不成立,直线另一侧区域就是不等式
不成立,直线另一侧区域就是不等式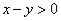 所表示的平面区域;将
所表示的平面区域;将 代入,即
代入,即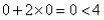 ,不等式
,不等式 成立,则原点所在区域就是不等式
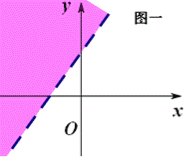
成立,则原点所在区域就是不等式 所表示的平面区域.(图一)
所表示的平面区域.(图一)
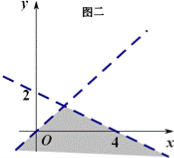
④求公共部分:如图二所示公共部分就是不等式组所表示的平面区域.
方法二:法向量判定法
由平面解析几何知识知道直线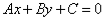 (
(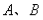 不同时为0)的一个法向量为
不同时为0)的一个法向量为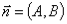 .以坐标原点作为法向量的始点,可以利用向量内积证明如下结论:
.以坐标原点作为法向量的始点,可以利用向量内积证明如下结论:
(1)不等式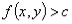 (
(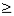 ),不等式表示的平面区域就是法向量指向的区域;(大于同向)
),不等式表示的平面区域就是法向量指向的区域;(大于同向)
(2)不等式 (
(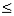 ),不等式表示的平面区域就是法向量反向的区域;(小于反向)
),不等式表示的平面区域就是法向量反向的区域;(小于反向)
例2 画出不等式组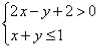 所表示的平面区域.
所表示的平面区域.
解析:①不等式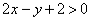 对应的直线方程是
对应的直线方程是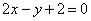 ,法向量
,法向量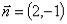 ;不等式
;不等式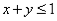 对应的直线方程是
对应的直线方程是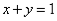 ,法向量
,法向量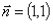 ;在平面直角坐标系中作出直线
;在平面直角坐标系中作出直线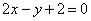 与
与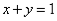 及其相应的法向量(如图).
及其相应的法向量(如图).


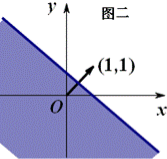
②由于不等式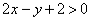 (
(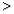 ),平面区域是法向量
),平面区域是法向量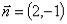 指向的区域(图一);不等式
指向的区域(图一);不等式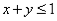 (
(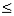 ),平面区域是法向量
),平面区域是法向量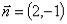 反向的区域(图二).
反向的区域(图二).
③然后求的公共部分就是不等式组所表示的平面区域.
方法三:未知数系数化正法
直线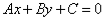 (
(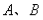 不同时为0)含有两个未知数,于是我们可以将未知数的系数分为两类:
不同时为0)含有两个未知数,于是我们可以将未知数的系数分为两类: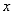 项系数与
项系数与 项系数来研究.
项系数来研究.
(1) 项系数化正法:顾名思义就是利用不等式性质,不等号两边同时
项系数化正法:顾名思义就是利用不等式性质,不等号两边同时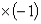 (移项)将
(移项)将 项系数化为正值,然后根据变形后关于
项系数化为正值,然后根据变形后关于 的不等式中的不等号来确定区域位置(规定:
的不等式中的不等号来确定区域位置(规定: 轴正方向所指的区域为直线的上方;反之为下方)有结论:
轴正方向所指的区域为直线的上方;反之为下方)有结论:
 项系数正值化:
项系数正值化: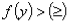 上;
上; 下.
下.
例3 画出不等式组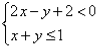 所表示的平面区域.
所表示的平面区域.
解析:①不等式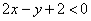 对应的直线方程是
对应的直线方程是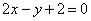 ;不等式
;不等式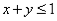 对应的直线方程是
对应的直线方程是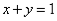 ;在平面直角坐标系中作出直线
;在平面直角坐标系中作出直线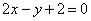 与
与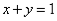 (如图).
(如图).
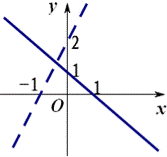

②将不等式组中每个不等式 项系数正值化,得
项系数正值化,得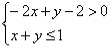 或
或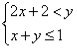 (移项).
(移项).
③关于 的不等式(
的不等式(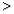 )即
)即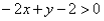 (或者
(或者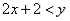 ),直线上方的区域就是该不等式所表示的平面区域(图一);关于
),直线上方的区域就是该不等式所表示的平面区域(图一);关于 的不等式(
的不等式(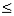 )即
)即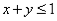 ,直线下方的区域就是该不等式所表示的平面区域(图二).
,直线下方的区域就是该不等式所表示的平面区域(图二).
④然后求的公共部分就是不等式组所表示的平面区域.
(2)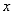 项系数化正法:同(1)一样,不等号两边同时
项系数化正法:同(1)一样,不等号两边同时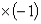 (或移项)将
(或移项)将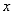 项系数化为正值,然后根据变形后关于
项系数化为正值,然后根据变形后关于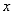 的不等式中的不等号来确定区域位置(规定:
的不等式中的不等号来确定区域位置(规定: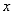 轴正方向所指的区域为直线的右方;反之为左方)有结论:
轴正方向所指的区域为直线的右方;反之为左方)有结论:
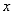 项系数正值化:
项系数正值化: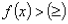 右;
右; 左.
左.
可结合例3来对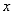 项系数化正法进行理解.
项系数化正法进行理解.
上述方法中,方法一是寻找二元一次不等式所表示的平面区域的常规方法,思维回路较长,适合对理论的学习,但要快速准确地解决简单的线性规划问题就必须掌握方法二或方法三中之一.
小编推荐
1.2025年开设农村区域发展专业大学排名及评级 高校排行榜