韦达定理公式变形6个 有哪些恒等变形

法国数学家弗朗索瓦·韦达在著作《论方程的识别与订正》中建立了方程根与系数的关系，由于韦达最早发现了这种关系，人们把这个关系称为韦达定理。我们在使用韦达定理进行解题时，经常会对一些代数进行恒等变形，具体如下。

韦达定理公式变形

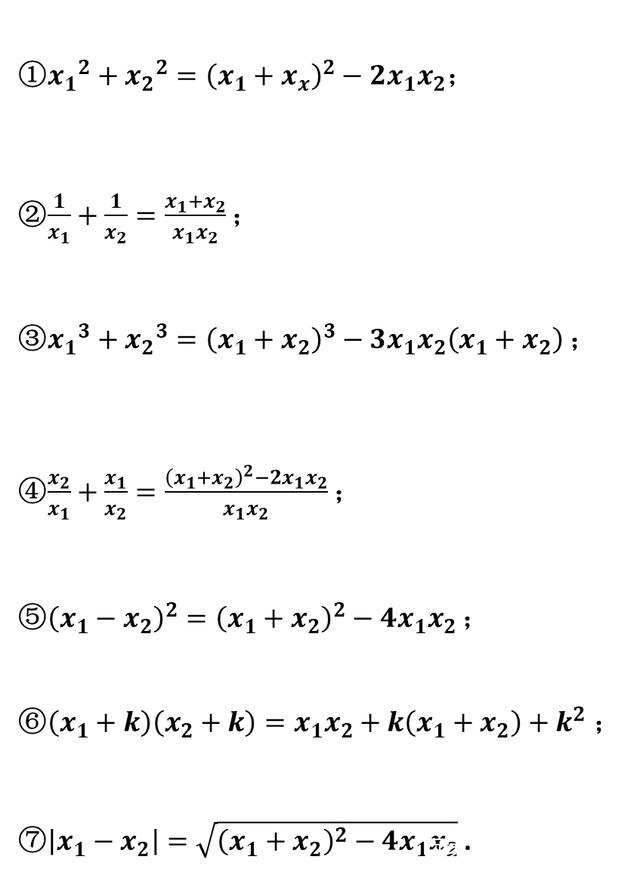
韦达定理的定义

韦达定理在求根的对称函数，讨论二次方程根的符号、解对称方程组以及解一些有关二次曲线的问题都凸显出独特的作用。

根的判别式是判定方程是否有实根的充要条件，韦达定理说明了根与系数的关系。无论方程有无实数根，实系数一元二次方程的根与系数之间适合韦达定理。判别式与韦达定理的结合，则更有效地说明与判定一元二次方程根的状况和特征。

小编推荐

1.青岛大学国际本科报名需要多少分 有哪些项目

2.广东历史类568分能考哪些大学 2025考生稳上的大学名单

3.2025男孩色弱上大学能选哪些专业 什么专业有前途

4.2025年455分能考什么师范类大学 哪些大学值得报

5.青海文科238分能考哪些大学 2025考生稳上的大学名单

6.2025贵州624分能上的大学有哪些 可以报考院校名单

7.国际生申请香港理工商科本科条件 有哪些要求

8.宁夏文科553分能考哪些大学 2025考生稳上的大学名单