高中不等式的基本性质：（一）对称性。（二）传递性。（三）加法单调性，即同向不等式可加性。（四）乘法单调性。（五）同向正值不等式可乘性。（六）正值不等式可乘方。（七）正值不等式可开方。（八）倒数法则。
高中不等式的基本性质
1.如果x>y，那么y<x；如果y<x，那么x>y；（对称性)
2.如果x>y，y>z；那么x>z；（传递性）
3.如果x>y，而z为任意实数或整式，那么x+z>y+z,即不等式两边同时加或减去同一个整式，不等号方向不变;
4.如果x>y，z>0，那么xz>yz ,即不等式两边同时乘以（或除以）同一个大于0的整式，不等号方向不变;
5.如果x>y，z<0，那么xz<yz, 即不等式两边同时乘以（或除以）同一个小于0的整式，不等号方向改变;
6.如果x>y，m>n，那么x+m>y+n；
7.如果x>y>0，m>n>0，那么xm>yn；
8.如果x>y>0，那么x的n次幂>y的n次幂（n为正数)，x的n次幂<y的n次幂（n为负数）。
或者说，不等式的基本性质的另一种表达方式有：
①对称性；
②传递性；
③加法单调性，即同向不等式可加性；
④乘法单调性；
⑤同向正值不等式可乘性；
⑥正值不等式可乘方；
⑦正值不等式可开方；
⑧倒数法则。
如果由不等式的基本性质出发，通过逻辑推理，可以论证大量的初等不等式。
各种常用不等式汇总
数学中有一些常用的不等式，它们形式优美且有重要的应用价值。
1、均值不等式：对任意的正整数n>1，正数的算术平均数不小于几何平均数。
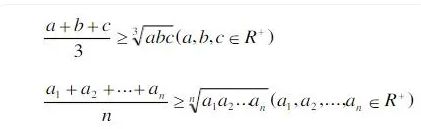
2、伯努利不等式：对任意的正整数n>1,以及任意的x>-1，有
证明：采用数学归纳法：n=1时，不等式明显成立，我们假设当n=k-1时，不等式成立，那么
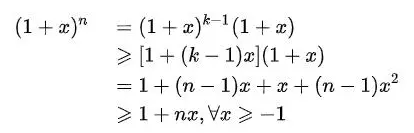
3、绝对值不等式：a、b是实数，则
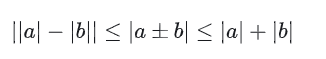
4、二项式展开式，可以用来放大缩小数列，求极限
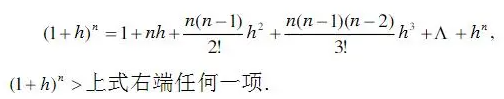
此外还有很多难些的不等式，例如数学分析到泛函分析里最最重要的一些不等式：柯西-施瓦茨不等式、Jesen不等式、赫尔德（Holder）不等式、闵可夫斯基（Minkowski）不等式、Hilbert空间的贝塞尔不等式，Poincare不等式（变分学中非常重要的不等式）等等。
小编推荐
下载文档