椭圆切线方程公式推导

椭圆方程为x²/a²+y²/b²=1,对x求导可得：2x/a²+2yy'/b²=0,因此椭圆上任意一点(x,y)处的切线斜率k=y'=-b²x/(a²y)；若M(x₀,y₀)为椭圆上任意一点,则过M的切线方程为：y=[-b²x₀/(a²y₀)](x-x₀)+y₀。

椭圆切线方程公式的推导过程

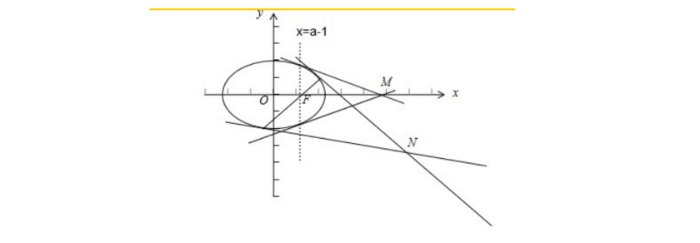
直线与椭圆的位置关系

直线与椭圆的位置关系分为三种：相离、相切、相交。

1.直线与椭圆相离的充要条件是直线与椭圆的方程组成的方程组无解,即所得一元二次方程的根的判别式小于0。

2.直线与椭圆相切的充要条件是直线与椭圆的方程组成的方程组有唯一解,即所得一元二次方程的根的判别式等于0。

3.直线与椭圆相交的充要条件是直线与椭圆的方程组成的方程组有两个不同的解,即所得一元二次方程的根的判别式大于0。

小编推荐

1.因式分解法解一元二次方程

2.高温煅烧石灰石的化学方程式

3.二元一次方程详细解法

4.无氧呼吸的两个阶段的方程式

5.初中二次函数求根公式是什么

6.钠与水反应离子方程式

7.相对分子质量计算公式

8.椭圆焦点三角形面积公式