定义区间和定义域的差别

定义域是某一个函数固定而且一定满足要求的一个x的取值范围。定义区间是根据题目来限定这个函数的x的取值的。

定义域是函数三要素(定义域、值域、对应法则）之一，对应法则的作用对象。求函数定义域主要包括三种题型：抽象函数，一般函数，函数应用题。含义是指自变量x的取值范围。

定义域定义

定义一：设x、y是两个变量，变量x的变化范围为D，如果对于每一个数x∈D，变量y遵照一定的法则总有确定的数值与之对应，则称y是x的函数，记作y=f(x)，x∈D，x称为自变量，y称为因变量，数集D称为这个函数的定义域。

定义二：A，B是两个非空数集，从集合A到集合B的一个映射，叫做从集合A到集合B的一个函数。记作

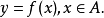
或

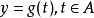
其中A就叫做定义域。通常，用字母D表示。通常定义域是F(X)中x的取值范围。

1、给定定义域：例如：函数

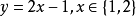
的定义域为给定的集合{1,2}。

2、一般函数的定义域：使函数有意义的一切实数。例如：函数y=1/x的定义域为

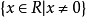
R为任意实数。也可以写做

3、实际问题：根据具体情况求定义域。

4、当然，也会运用到动力物理学中求变量。

定义区间

若在实数集中，在某个区间上的函数都是有定义的，则这个区间就称为“定义区间”，孤立的点构不成区间。

小编推荐

1.入党和没入党的差别？如何才能顺利入党？

2.高三一般比高二成绩好还是差 差别大吗

3.导数的定义式

4.2023民办本科有必要读吗 与公办本科有什么差别

5.2023高考报志愿冲刺区间 有什么冲刺技巧

6.2023强基计划各省招生人数差别大吗

7.amsr和asmr的差别

8.什么是三角函数 定义是什么